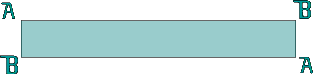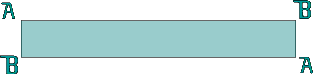Proprietati ale benzii
lui Möbius:
Doua puncte se
zice ca sunt pe aceeasi fata daca se pot uni printr-o linie curba care sa
nu sara vreo margine.
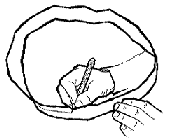
Trasati o linie pe
mijlocul benzii, fara a ridica creionul de pe banda. Nu va opriti pana nu
ajungeti din nou in punctul din care ati pornit. (nu va faceti griji ca linia
nu a iesit perfect dreapta, ideea principala este sa nu sara marginea)
Constatati ca
linia este trasa pe ambele parti, si ca din orice punct al benzii se poate
ajunge la linie. Asadar, ca sa unim doua puncte oarecare ale suprafetei benzii,
A si B, pornind din A, este suficient sa unim A cu linia, sa mergem pe linie
pana in dreptul lui B, apoi sa unim linia cu B. Deci, suprafata are O SINGURA
FATA.
Cu o carioca colorati
punctele de margine, fara sa ridicati carioca de pe muchie, pana cand ajungeti
in punctul din care ati plecat.
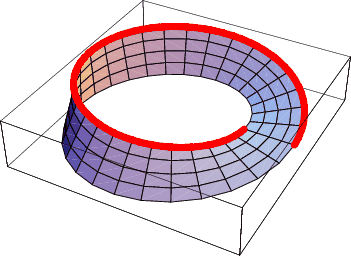
Constatati ca toate
punctele de margine ale benzii sunt colorate. Deci, suprafata are O SINGURA
MUCHIE.
Asadar, banda lui Möbius este o suprafata cu o singura fata si o singura
muchie, simplu rasucita.
Ce se intampla
cu o foaie de hartie, daca o taiati pe jumatate? Se imparte in doua jumatati
de doua ori mai inguste. Ce se intampla cu banda lui Möbius, daca o taiati
pe jumatate?
Taiati banda dupa linia
de pe mijlocul ei. (nu este grav daca nu puteti urmari linia intocmai, important
este sa taiati de-a lungul benzii, nu de-a latul.)
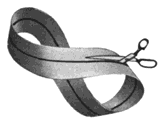

Constatati ca
obtineti o singura banda, de doua ori mai lunga.
Cate fete are?
Trasati cu creionul o linie pe mijlocul benzii, pana cand ajungeti din nou
de unde ati plecat. Constatati ca linia este trasa doar pe o parte, ceea ca
inseamna ca s-a obtinut o suprafata cu DOUA FETE.
Cate muchii are?
Ca si mai inainte, colorati cu o carioca punctele de margine, fara a
ridica carioca de pe foaie. Constatati ca a ramas o margine necolorata, adica
s-a obtinut o suprafata cu DOUA MARGINI.
Cate rasuciri are?
DOUA.
Asadar, prin taierea
de-a lungul a benzii lui Möbius se obtine o suprafata cu doua fete si
doua margini, dublu rasucita.
Ce se obtine prin sectionarea
acestei benzi de-a lungul ei? Acesata noua banda respecta toate proprietatile
suprafetelor cu doua fete (de exemplu, ale benzii de hartie din care s-a construit
banda lui Möbius): taiata pe jumatate, se obtin 2 benzi de acceeasi lungime,
cu doua fete, cu doua muchii, dublu rasucite, dar de doua ori mai inguste
(de 4 ori mai inguste decat banda lui Möbius). Doar ca sunt legate ca
zalele unui lant. Si fiecare dintre ele, taiata de-a lungul, se desparte in
doua benzi de aceeasi lungime, cu doua fete, cu doua muchii, dublu rasucite,
dar de doua ori mai inguste decat banda din care s-au obtinut.
Creati o alta banda
a lui Möbius. Alegeti un punct care sa nu fie pe mijlocul benzii (de
exemplu, cam la o treime din latimea benzii) si trasati o linie paralela cu
marginile (de-a lungul benzii). Cate benzi obtineti daca taiati acum banda
dupa linia pe care ati trasat-o?
Taiati banda dupa linia
trasata. Constatati ca s-au obtinut DOUA benzi. Verificati-le proprietatile.
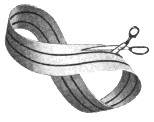

Cea
obtinuta in mijloc este tot o banda a lui Möbius, adica o suprafata cu
2 fete, 2 muchii, simplu rasucita, dar de latime mai mica decat banda initiala.
Cealalta, obtinuta "pe margine", este o suprafata cu 2 fete, 2 muchii,
dublu rasucita si de doua ori mai lunga.
***
Ce se intampla daca,
atunci cand creati banda lui Möbius, in loc de o singura rasucire, ati
fi incercat o tripla rasucire?
S-ar fi obtinut tot o suprafata cu o singura fata si o singura muchie. Incercati
scum sectionarea acestei benzi de-a lungule ei. Ce obtineti? Ce proprietati
regasiti?
***
Banda lui Möbius
este cea mai simplã dintre structurile cu o singura fata. Luati o banda
de hartie mai lunga si colorati colturile opuse ale unei fete cu aceeasi culoare.
Puteti acum innoda aceasta banda oricum vreti, dar daca aveti grija sa suprapuneti
culorile, veti obtine o suprafata cu o singura fata si o singura muchie.
Mai jos sunt reprezentate
cateva noduri simple - suprafete cu o singura fata. Verificati-le proprietatile.
Prin sectionare se obtin suprafete foarte ciudate.
Pentru curiosii
de profesie, si cei care nu s-au speriat inca,
aici este reprezentarea matematica a benzii.